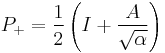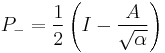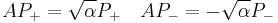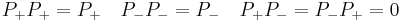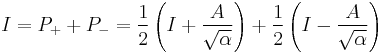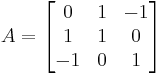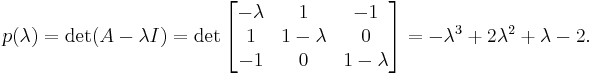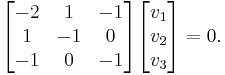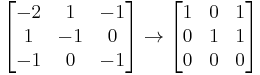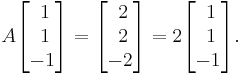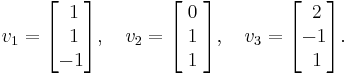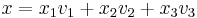Eigenvalue algorithm
In linear algebra, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.
Contents |
Characteristic polynomial
Given a square matrix A, an eigenvalue λ and its associated eigenvector v are, by definition, a pair obeying the relation
where v is nonzero. Equivalently, (A−λI)v = 0 (where I is the identity matrix), implying det(A−λI) = 0. This determinant is a polynomial in λ, known as the characteristic polynomial of A. One common method for determining the eigenvalues of a small matrix is by finding roots of the characteristic polynomial.
Unfortunately, this method has some limitations. A general polynomial of order n > 4 cannot be solved by a finite sequence of arithmetic operations and radicals (see Abel–Ruffini theorem). There do exist efficient root-finding algorithms for higher order polynomials. However, finding the roots of the characteristic polynomial may be an ill-conditioned problem even when the underlying eigenvalue problem is well-conditioned. For this reason, this method is rarely used.
The above discussion implies a restriction on all eigenvalue algorithms. It can be shown that for any polynomial, there exists a matrix (see companion matrix) having that polynomial as its characteristic polynomial (actually, there are infinitely many). If there did exist a finite sequence of arithmetic operations for exactly finding the eigenvalues of a general matrix, this would provide a corresponding finite sequence for general polynomials, in contradiction of the Abel–Ruffini theorem. Therefore, general eigenvalue algorithms are expected to be iterative.
Power iteration
Let the eigenvalues of  be
be 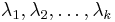 . Assume that
. Assume that 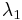 has absolute value strictly larger than that of
has absolute value strictly larger than that of  . This is an essential restriction: for a matrix with real coefficients, if the eigenvalue with highest absolute value is not real, its complex conjugate is also an eigenvalue (with the same absolute value).
. This is an essential restriction: for a matrix with real coefficients, if the eigenvalue with highest absolute value is not real, its complex conjugate is also an eigenvalue (with the same absolute value).
With the preceding assumptions in mind, the idea of the method is to choose an (arbitrary) unit length vector  and then repeatedly multiply it by the matrix
and then repeatedly multiply it by the matrix  and re-scale. One carries out the computation
and re-scale. One carries out the computation 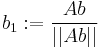 ,
, 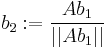 ,
, 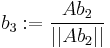 , .... Let the vector
, .... Let the vector  have a generalized eigenspace decomposition
have a generalized eigenspace decomposition 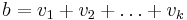 , where
, where 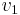 belongs to the generalized eigenspace corresponding to eigenvalue
belongs to the generalized eigenspace corresponding to eigenvalue 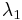 ,
, 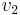 belongs to the generalized eigenspace corresponding to eigenvalue
belongs to the generalized eigenspace corresponding to eigenvalue 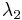 , etc. Each iteration of the algorithm will decrease the "contribution" of the components in the eigenspaces of eigenvalues
, etc. Each iteration of the algorithm will decrease the "contribution" of the components in the eigenspaces of eigenvalues  relative to the contribution of
relative to the contribution of 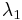 and therefore the vector
and therefore the vector 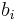 will converge to a unit eigenvector of eigenvalue
will converge to a unit eigenvector of eigenvalue 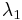 .
.
The power iteration algorithm for finding the (largest) eigenvalue is simple to implement but is otherwise not very useful in practice. Its convergence is slow except for special cases of matrices. Without modification, it can only find the dominant eigenvalue (and the corresponding eigenvector), provided they exist.
A few of the more advanced eigenvalue algorithms are variations of power iteration. In addition, some of the better algorithms for the generalized eigenvalue problem are based on power iteration.
Matrix eigenvalues
In mathematics, and in particular in linear algebra, an important tool for describing eigenvalues of square matrices is the characteristic polynomial: saying that λ is an eigenvalue of A is equivalent to stating that the system of linear equations (A - λI) v = 0 (where I is the identity matrix) has a non-zero solution v (namely an eigenvector), and so it is equivalent to the determinant det (A - λI) being zero. The function p(λ) = det (A - λI) is a polynomial in λ since determinants are defined as sums of products. This is the characteristic polynomial of A: the eigenvalues of a matrix are the zeros of its characteristic polynomial.
It follows that we can compute all the eigenvalues of a matrix A by solving the equation 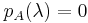 . If A is an n-by-n matrix, then
. If A is an n-by-n matrix, then 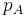 has degree n and A can therefore have at most n eigenvalues. Conversely, the fundamental theorem of algebra says that this equation has exactly n roots (zeroes), counted with multiplicity. All real polynomials of odd degree have a real number as a root, so for odd n, every real matrix has at least one real eigenvalue. In the case of a real matrix, for even and odd n, the non-real eigenvalues come in conjugate pairs.
has degree n and A can therefore have at most n eigenvalues. Conversely, the fundamental theorem of algebra says that this equation has exactly n roots (zeroes), counted with multiplicity. All real polynomials of odd degree have a real number as a root, so for odd n, every real matrix has at least one real eigenvalue. In the case of a real matrix, for even and odd n, the non-real eigenvalues come in conjugate pairs.
An example of a matrix with no real eigenvalues is the 90-degree rotation
whose characteristic polynomial is 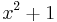 and so its eigenvalues are the pair of complex conjugates i, -i.
and so its eigenvalues are the pair of complex conjugates i, -i.
The Cayley–Hamilton theorem states that every square matrix satisfies its own characteristic polynomial, that is, 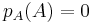 .
.
Types
Eigenvalues of 2×2 matrices
An analytic solution for the eigenvalues of 2×2 matrices can be obtained directly from the quadratic formula: if
then the characteristic polynomial is
so the solutions are
Notice that the characteristic polynomial of a 2×2 matrix can be written in terms of the trace  and determinant
and determinant 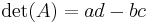 as
as
where 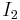 is the 2×2 identity matrix. The solutions for the eigenvalues of a 2×2 matrix can thus be written as
is the 2×2 identity matrix. The solutions for the eigenvalues of a 2×2 matrix can thus be written as
Thus, for the very special case where the 2×2 matrix has zero determinant, but non-zero trace, the eigenvalues are zero and the trace (corresponding to the negative and positive roots, respectively). For example, the eigenvalues of the following matrix are 0 and (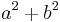 ):
):
This formula holds for only a 2×2 matrix.
Eigenvalues of 3×3 matrices
If
then the characteristic polynomial of A is
Alternatively the characteristic polynomial of a 3×3 matrix can be written in terms of the trace 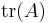 and determinant
and determinant 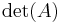 as
as
where 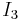 is the 3×3 identity matrix.
is the 3×3 identity matrix.
The eigenvalues of the matrix are the roots of this polynomial, which can be found using the method for solving cubic equations.
A formula for the eigenvalues of a 4×4 matrix could be derived in an analogous way, using the formulae for the solutions of the quartic equation.
A programmatical approach to finding eigenvalues
In case you don’t have access to scientific software that has an eigenvalue function, below are a set of steps you could use as pseudo code to help you create a program to solve problems.
For a 2×2:
//we know there are two eigenvalues, so the equations from above can be hard-coded in with minimal effort Eig11 = (a+d)/2 + sqrt(((a+d)*(a+d))/4 + bc – ad) Eig12 = (a+d)/2 - sqrt(((a+d)*(a+d))/4 + bc – ad) //eig11 is the value found using + and eig12 is the value using - //or we get the same two eigenvalues with the modified equation Eig21 = (a+d)/2 + sqrt(4bc + (a-d)(a-d))/2 Eig22 = (a+d)/2 - sqrt(4bc + (a-d)(a-d))/2
For a 3×3:
//a 3×3 is more complicated and requires several helper equations to accomplish due to the λ³ term. //These steps should help you calculate eigen values for a matrix that has ***3 REAL eigen values***. Define x,y,z //Use the equation from above to get your cubic equation and combine all constant terms possible to //give you a reduced equation we will use a, b, c and d to denote the coefficients of this equation. //Eqn = aλ³ + bλ² + cλ + d = 0 x = ((3c/a) – (b²/a²))/3 y = ((2b³/a³) – (9bc/a²) + (27d/a))/27 z = y²/4 + x³/27 Define I, j, k, m, n, p (so equations are not so cluttered) i = sqrt(y²/4 - z) j = -i^(1/3) k = arccos(-(y/2i)) m = cos(k/3) n = sqrt(3)*sin(k/3) p = b/3a Define Eig1, Eig2, Eig3 Eig1 = 2j*m + p Eig2 = -j *(m + n) + p Eig3 = -j*(m - n) + p
Eigenvalues of a Symmetric 3x3 Matrix
(Reference: Oliver K. Smith: Eigenvalues of a symmetric 3 × 3 matrix. Commun. ACM 4(4): 168 (1961) ) Note: this method does not work for singular matrices (matrices with one or more zero eigenvalues). This is a Matlab version:
% Given symmetric 3x3 matrix M, compute the eigenvalues m = trace(M)/3; K = M-m*eye(3); q = det(K)/2; p = 0 for i=1:3 for j=1:3 p = p + K(i,j)^2; end end p = p/6; phi = 1/3*acos(q/p^(3/2)); % NOTE: the follow formula assume accurate computation and therefor q/p^(3/2) should be in range of [1,-1], % but in real code, because of numerical errors, it must be checked. Thus, in case abs(q) >= abs(p^(3/2)), set phi = 0; if(abs(q) >= abs(p^(3/2))) phi = 0; end if(phi<0) phi=phi+pi/3; end eig1 = m + 2*sqrt(p)*cos(phi) eig2 = m - sqrt(p)*(cos(phi) + sqrt(3)*sin(phi)) eig3 = m - sqrt(p)*(cos(phi) - sqrt(3)*sin(phi))
Or here is a version in python that uses numpy:
def smith_eigenvals(mat): """Returns the eigenvalues of a 3x3 symmetric matrix. Or can use numpy.linalg.eigvals function. """ import numpy m = numpy.trace(mat) / 3. K = mat - m*numpy.eye(3) q = numpy.linalg.det(K) / 2. p = numpy.sum(K*K) / 6. # NB in Smith's paper he uses phi = (1./3.)*arctan(sqrt(p**3 - q**2)/q), which is equivalent to below: phi = (1./3.)*numpy.arccos(q/(p**(3./2.))) print "m", m print "p", p print "q", q print "phi", phi if abs(q) >= abs(p**(3./2.)): phi = 0. if phi < 0.: phi = phi + numpy.pi/3. eig1 = m + 2.*numpy.sqrt(p)*numpy.cos(phi) eig2 = m - numpy.sqrt(p)*(numpy.cos(phi) + numpy.sqrt(3.)*numpy.sin(phi)) eig3 = m - numpy.sqrt(p)*(numpy.cos(phi) - numpy.sqrt(3.)*numpy.sin(phi)) return eig1, eig2, eig3
Eigenvalues and eigenvectors of special matrices
For matrices satisfying 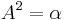 one can write explicit formulas for the possible eigenvalues and the projectors on the corresponding eigenspaces.
one can write explicit formulas for the possible eigenvalues and the projectors on the corresponding eigenspaces.
with
and
This provides the following resolution of identity
The multiplicity of the possible eigenvalues is given by the rank of the projectors.
Example computation
The computation of eigenvalue/eigenvector can be realized with the following algorithm.
Consider an n-square matrix A
- 1. Find the roots of the characteristic polynomial of A. These are the eigenvalues.
- If n different roots are found, then the matrix can be diagonalized.
- 2. Find a basis for the kernel of the matrix given by
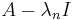 . For each of the eigenvalues. These are the eigenvectors
. For each of the eigenvalues. These are the eigenvectors
- The eigenvectors given from different eigenvalues are linearly independent.
- The eigenvectors given from a root-multiplicity are also linearly independent.
Let us determine the eigenvalues of the matrix
which represents a linear operator R³ → R³.
Identifying eigenvalues
We first compute the characteristic polynomial of A:
This polynomial factors to 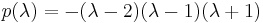 . Therefore, the eigenvalues of A are 2, 1 and −1.
. Therefore, the eigenvalues of A are 2, 1 and −1.
Identifying eigenvectors
With the eigenvalues in hand, we can solve sets of simultaneous linear equations to determine the corresponding eigenvectors. Since we are solving for the system 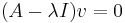 , if
, if 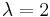 then,
then,
Now, reducing 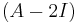 to row echelon form:
to row echelon form:
allows us to solve easily for the eigenspace 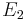 :
:
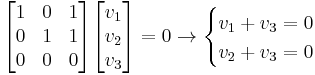
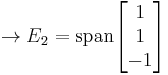 .
.
We can confirm that a simple example vector chosen from eigenspace 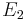 is a valid eigenvector with eigenvalue
is a valid eigenvector with eigenvalue 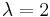 :
:
Note that we can determine the degrees of freedom of the solution by the number of pivots.
If A is a real matrix, the characteristic polynomial will have real coefficients, but its roots will not necessarily all be real. The complex eigenvalues come in pairs which are conjugates. For a real matrix, the eigenvectors of a non-real eigenvalue z , which are the solutions of 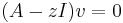 , cannot be real.
, cannot be real.
If v1, ..., vm are eigenvectors with different eigenvalues λ1, ..., λm, then the vectors v1, ..., vm are necessarily linearly independent.
The spectral theorem for symmetric matrices states that if A is a real symmetric n-by-n matrix, then all its eigenvalues are real, and there exist n linearly independent eigenvectors for A which are mutually orthogonal. Symmetric matrices are commonly encountered in engineering.
Our example matrix from above is symmetric, and three mutually orthogonal eigenvectors of A are
These three vectors form a basis of R³. With respect to this basis, the linear map represented by A takes a particularly simple form: every vector x in R³ can be written uniquely as
and then we have
Advanced methods
A popular method for finding eigenvalues is the QR algorithm, which is based on the QR decomposition. Besides, combining Householder transformation with LU decomposition can get better convergence than QR algorithm. [1] Other advanced methods include:
- Inverse iteration
- Rayleigh quotient iteration
- QR algorithm
- Arnoldi iteration
- Lanczos iteration
- Jacobi method
- Bisection
- Divide-and-conquer
Most eigenvalue algorithms rely on first reducing the matrix A to Hessenberg or tridiagonal form. This is usually accomplished via reflections.
See also
Notes
|
||||||||||||||
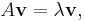
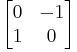
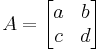
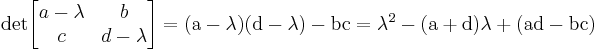
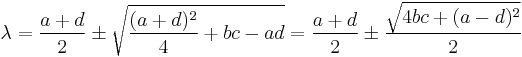
![{\rm det} \begin{bmatrix} a-\lambda & b \\ c & d-\lambda \end{bmatrix}
= {\rm det} \left[ A - \lambda I_{2}\right]
= \lambda^2- \lambda {\rm tr}(A)%2B {\rm det}(A)](/2012-wikipedia_en_all_nopic_01_2012/I/8585dff6ae72056f07ae95a6a4041126.png)
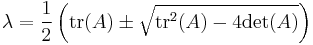
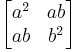
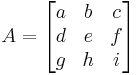
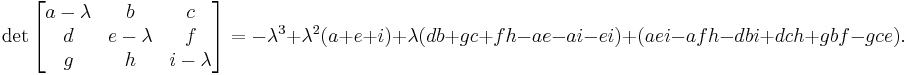
![{\rm det} \left[ A - \lambda I_{3}\right]
= -\lambda^3
%2B \lambda^2 {\rm tr}(A)
%2B \lambda \frac{1}{2}\left[ {\rm tr}(A^2) - {\rm tr}^2(A) \right]
%2B {\rm det}(A)](/2012-wikipedia_en_all_nopic_01_2012/I/6e9aa40d78e235a9634ef13a890fee95.png)